entee memo
Jump to navigation�������ɿ������Ƚ
�����ָ����ȱ����줿���פȼ����Ū�ķ����� [3]
�����ʲ��ˡ� ��������ˤβ��뵷
��������ˤβ��뵷����ã���뤿��ΰ���Ū��ˡ��ʲ��˼�����
�ʤ��β��ˤ��Τ褦��̵��̣�ʥ֥��������ΤϤʤ����������ԻĤ����֥����ΥХ���������Ȥ�ɽ�����줿���Ȥ��������Զ�礫����
�����ɤ����ˤϤ���ɽ�������ǡ������ο���������ΤɤΤ褦�ʥ��ݥå��ˤ��줾���б����Ƥ���Τ���ֻ��ˤ�������Ǥ��뤫�⤷��ʤ����Ȥ�櫓�����裳���פˤ������������ơ�����ƶᴶ��Ф�������¿����������Ʊ�������¤٤�Ȥ�����Ū��ħ�Ȥ�����Τϡ������λ���˱����ƶˤ�ƽ��פʰ�̣����Ĥ���Ǥ��롣�裱�����Ĥο����ˤ�ä�ɽ�����裲������Ĥο����ˤ�ä�ɽ�����������裳���Ĥο����ˤ�ä�ɽ�����Ȥˤ�äơ����줾��ο������ɤμ����°���뤫��ɽ����������ʤ��������֤����������Τ����μ���ˤ��������Ū�ֻ����פ�ɽ�����롣���Υ����ƥ�ϼ¤����ˤ��ʤä���ΤǤ��롣
�����������ǤϤ��ΤҤȤĤҤȤĤΰ�̣�Ȥ�����б��������Ū����˾�Υ��ݥå������Ǥ���Τ���ܽҤ��ʤ�������Ϥ��줫���ɤäƾܤ������Ƥ�������Ǥ��롣����ϡ������ο���������ӥ�������ɽ����뤳�Ȥˤ�äƤϻ����Ķ��������������������ʤ��ȸ������ȤǤ��롣
���ʤ��������ӥ��������ɤ�ʤ��͡��ˤȤäƤϡ��ʤ��ΰ�̣��ʤ��ֵ���餷����Ρפη����֤���¾�ʤ�ʤ��������η����ˤϻ����Ķ����ǧ�����������Ρʤ�Ȥ�ȤϤ��ä��Τ��⤷��ʤ�������������Ϥ伺����¸�ߤ��ʤ�����Ǥ��롣���ʤ��Ȥⷫ���֤������뤳�Ȥϻ�ǧ����褦���������ˤɤ�ʰ�̣������Τ����ɤ߲Τ����Ǥ��������ʤ�С����μ¤ˤ��줬������ɽ���Ƥ�����¤������뤿��ˤϡ������Ķ����¸�ߤ����Τ�ɽ�ݤ���Ѥ�����ˡ��ͭ���Ȥʤ롣�����˴�����Ū��������Ķ����¸�ߤ��륷�˥ե�����ʵ���ɽ���ˤȤ��Ƥ�ħ�κ��Ѥ���Ƥ����롣
�֤Ǥ���в֤Ӥ�ο����դǤ���Ф��η������ֿ����פ�ɽ������Ȥ��Ƶ�ǽ������ɤ��ΤǤ��ꡢ���ξ�硢�����仰���դΥ������С��ϡȣ��ɤ�ɽ������Ȥ��ơ�������β֤ϡȣ��ɤ�ɽ������Ȥ��ơ����β֤ϡ���������������ǡʡȣ��ɤʤ����ˡȣ��ɤ�ɽ������Ȥ��ơ����Ѳ�ǽ�ʤΤǤ��롣�Ĥޤꡢ�����ǡֻ����դΥ������С��פϥ��˥ե�����Ǥ��ꡢ�֣��פȤ������������˥ե����Ǥ��롣���ˡ�����λ��ͤ���۲�ã�ϡ��֤��̣�������뤿������̤ʵ���Ȥ��ƻ��Ѥ����褿���㤬���롣
���ơ��ʾ�θ�����������ӥ����Ȥ鷺������Ū��ã��ޤ����Ȥ������ΰ���Ū��ˡ�ϰʲ��Τ褦�ˤʤ롣�����ε���ϰ���Ǥ��ꡢ���ޤ��ޤʥХꥨ�������¸�ߤ��롣�����ǤϤҤȤĤ��Ϸ�����α�ᡢ��Ū������ҤȤĤҤȤĴѤƹԤ����ˡ������ΥХꥨ��������Ѥ뤳�Ȥˤʤ�Ǥ�������
�����ͼ��������������ʥ���å����Ƴ����
����ˤ����Ƥϥ��ƥ�ɥ��饹�Υ�����ɥ��������ʤؤ����� �˥å��ˡ�������Ʃ����Ħ�����η����ʤɤˤ�äƤ��ο������������������ơ���������������μ¤�����ο��Ȥ�����ã�������οʹ֤������뤿��ˡ������������������Ū���Ѥ�ɬ�פȤʤ롣���Ѥ����ۤɤˡ���������̤ʰ�̣����������Ф��ƿ͡����ؿ���ʧ��ʤ��ʤ뤫��Ǥ��롣�������äƿ����Τ�Τ����ʤ��ΤǤ��ꡢ���ߤʿ������ɽ�ݤ����Ѥ���Ѥ������ɬ�פ����ä���
���Τ褦�ʤ櫓�ǡ����ã�����Ϥˤ�ꤳ�������������ݻ�������ɽ��Ū�о�ʪ���Τ��ưפ����Ѻ��ʤ��о줹����Ϥʤ������̤���ͳ�����Τ���Ū������������о줹�뤳�Ȥˤʤ롣�դ˸����С����������������������륷�˥ե�����Ȥ��Ƥ�ɽ��ʪ���о줹��Ȥ������줬̵��̣���о줹�뤳�ȤϤʤ��ä��ΤǤ��롣�μ¤˲����������뤿������ˤ�����������ɽ�ݤ������褦�ˤʤ롣
���٤���Ͽ������Τ�ΤǤ��ꡢ�����Ͽ����������Ǥ��롣
�ʤ��β��ˤ��Τ褦��̵��̣�ʥ֥��������ΤϤʤ����������ԻĤ����֥����ΥХ���������Ȥ�ɽ�����줿���Ȥ��������Զ�礫����
|
�裱��
|
1 (8)
|
2
|
3
|
4
|
5
|
6
|
7
|
(8)
|
|
�裲��
|
11 (88)
|
22
|
33
|
44
|
55
|
66
|
77
|
(88)
|
|
�裳��
|
111 (888)
|
222
|
333
|
444
|
555
|
666
|
777
|
(888)
|
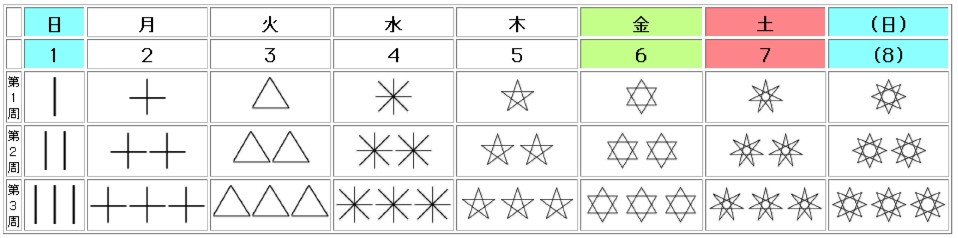
�����ɤ����ˤϤ���ɽ�������ǡ������ο���������ΤɤΤ褦�ʥ��ݥå��ˤ��줾���б����Ƥ���Τ���ֻ��ˤ�������Ǥ��뤫�⤷��ʤ����Ȥ�櫓�����裳���פˤ������������ơ�����ƶᴶ��Ф�������¿����������Ʊ�������¤٤�Ȥ�����Ū��ħ�Ȥ�����Τϡ������λ���˱����ƶˤ�ƽ��פʰ�̣����Ĥ���Ǥ��롣�裱�����Ĥο����ˤ�ä�ɽ�����裲������Ĥο����ˤ�ä�ɽ�����������裳���Ĥο����ˤ�ä�ɽ�����Ȥˤ�äơ����줾��ο������ɤμ����°���뤫��ɽ����������ʤ��������֤����������Τ����μ���ˤ��������Ū�ֻ����פ�ɽ�����롣���Υ����ƥ�ϼ¤����ˤ��ʤä���ΤǤ��롣
�����������ǤϤ��ΤҤȤĤҤȤĤΰ�̣�Ȥ�����б��������Ū����˾�Υ��ݥå������Ǥ���Τ���ܽҤ��ʤ�������Ϥ��줫���ɤäƾܤ������Ƥ�������Ǥ��롣����ϡ������ο���������ӥ�������ɽ����뤳�Ȥˤ�äƤϻ����Ķ��������������������ʤ��ȸ������ȤǤ��롣
���ʤ��������ӥ��������ɤ�ʤ��͡��ˤȤäƤϡ��ʤ��ΰ�̣��ʤ��ֵ���餷����Ρפη����֤���¾�ʤ�ʤ��������η����ˤϻ����Ķ����ǧ�����������Ρʤ�Ȥ�ȤϤ��ä��Τ��⤷��ʤ�������������Ϥ伺����¸�ߤ��ʤ�����Ǥ��롣���ʤ��Ȥⷫ���֤������뤳�Ȥϻ�ǧ����褦���������ˤɤ�ʰ�̣������Τ����ɤ߲Τ����Ǥ��������ʤ�С����μ¤ˤ��줬������ɽ���Ƥ�����¤������뤿��ˤϡ������Ķ����¸�ߤ����Τ�ɽ�ݤ���Ѥ�����ˡ��ͭ���Ȥʤ롣�����˴�����Ū��������Ķ����¸�ߤ��륷�˥ե�����ʵ���ɽ���ˤȤ��Ƥ�ħ�κ��Ѥ���Ƥ����롣
�֤Ǥ���в֤Ӥ�ο����դǤ���Ф��η������ֿ����פ�ɽ������Ȥ��Ƶ�ǽ������ɤ��ΤǤ��ꡢ���ξ�硢�����仰���դΥ������С��ϡȣ��ɤ�ɽ������Ȥ��ơ�������β֤ϡȣ��ɤ�ɽ������Ȥ��ơ����β֤ϡ���������������ǡʡȣ��ɤʤ����ˡȣ��ɤ�ɽ������Ȥ��ơ����Ѳ�ǽ�ʤΤǤ��롣�Ĥޤꡢ�����ǡֻ����դΥ������С��פϥ��˥ե�����Ǥ��ꡢ�֣��פȤ������������˥ե����Ǥ��롣���ˡ�����λ��ͤ���۲�ã�ϡ��֤��̣�������뤿������̤ʵ���Ȥ��ƻ��Ѥ����褿���㤬���롣
���ơ��ʾ�θ�����������ӥ����Ȥ鷺������Ū��ã��ޤ����Ȥ������ΰ���Ū��ˡ�ϰʲ��Τ褦�ˤʤ롣�����ε���ϰ���Ǥ��ꡢ���ޤ��ޤʥХꥨ�������¸�ߤ��롣�����ǤϤҤȤĤ��Ϸ�����α�ᡢ��Ū������ҤȤĤҤȤĴѤƹԤ����ˡ������ΥХꥨ��������Ѥ뤳�Ȥˤʤ�Ǥ�������

�����ͼ��������������ʥ���å����Ƴ����
����ˤ����Ƥϥ��ƥ�ɥ��饹�Υ�����ɥ��������ʤؤ����� �˥å��ˡ�������Ʃ����Ħ�����η����ʤɤˤ�äƤ��ο������������������ơ���������������μ¤�����ο��Ȥ�����ã�������οʹ֤������뤿��ˡ������������������Ū���Ѥ�ɬ�פȤʤ롣���Ѥ����ۤɤˡ���������̤ʰ�̣����������Ф��ƿ͡����ؿ���ʧ��ʤ��ʤ뤫��Ǥ��롣�������äƿ����Τ�Τ����ʤ��ΤǤ��ꡢ���ߤʿ������ɽ�ݤ����Ѥ���Ѥ������ɬ�פ����ä���
���Τ褦�ʤ櫓�ǡ����ã�����Ϥˤ�ꤳ�������������ݻ�������ɽ��Ū�о�ʪ���Τ��ưפ����Ѻ��ʤ��о줹����Ϥʤ������̤���ͳ�����Τ���Ū������������о줹�뤳�Ȥˤʤ롣�դ˸����С����������������������륷�˥ե�����Ȥ��Ƥ�ɽ��ʪ���о줹��Ȥ������줬̵��̣���о줹�뤳�ȤϤʤ��ä��ΤǤ��롣�μ¤˲����������뤿������ˤ�����������ɽ�ݤ������褦�ˤʤ롣
���٤���Ͽ������Τ�ΤǤ��ꡢ�����Ͽ����������Ǥ��롣
posted at 13:15:00 on 2006-02-06
by entee -
Category: �����������Ƚ
TrackBacks
������
No comments yet